Batch 3 - Class 180 - Rolling Tetrahedrons

• What is the color of the last square in the following rolling tetrahedron? (Intiial color of base is black)

• Answer: Black
• https://demonstrations.wolfram.com/ColoringThePlaneWithARollingTetrahedron/
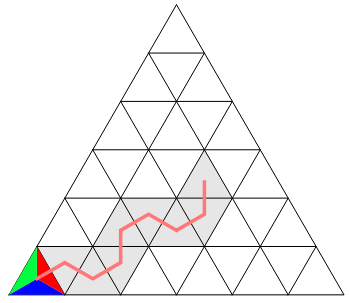
• Try this one

• Can you try to think of templates (how do you express all rules), so that this becomes easier. Think about what completely specifies the "input" and "output"
• How many configurations of the tetrahedron exist? Unique ones?
• Answer: 12 - you can choose the bottom and front.
• But since this arrangement also has inverted one, you may need another 12
• Or if you are willing to just rotate the template, then you need only 4
• How many moves are there for each configuration?
• Can you tabulate all of them?
• Is there a simpler pattern - look at where each color goes on a move, with respect to starting and resulting position.
• Try to take two different paths to the same destination position. Do you think you will land up with the same configuration at the end, or can it be different?
• Try it out for a few cases
• Can you think about why? Is there some underlying property which leads to this?
• Can you figure out when the same position recurs on the grid - is there a pattern?
• How many unique configurations actually exist on the grid (Answer: 8, arranged in a parallelogram, which then repeats itself infinitely)
• Find the color of target square if you roll the cubical dice below

• Can you think about the different paths to the same destination with a cubical dice? What does each column look like? What do successive columns look like? 
• Answer: In this case, different paths land up with different configurations at target cell. For example, a sequence of right-above-left-down moves gets back to the same cell in a different configuration.

• Take 4 consecutive integers and multiply them. Can you think of a sequence where the product is a perfect square?
• think why.